In my previous article, I discussed how to decide which model to use based on factors like sample size, feature types, and their quantity. This time, I want to shift focus to a more practical approach: choosing between algorithms with a clear goal in mind—whether it’s for trading or generating signals for further analysis.
This article might run a bit long, as I plan to delve into the underlying mathematics that supports the latter part of the discussion, ultimately addressing the central question. It’s worth noting that this piece is heavily inspired by several insightful posts on X, so I can only claim about 25% of the credit here.
Linear estimators part
To address the question posed in the article’s title, it’s helpful to start by highlighting the linear regressors commonly used by serious quants and traders:
Ordinary Least Squares (OLS)
Quantile Regression
Ridge Regression
The choice between these three often hinges on the nature of our data and the number of factors we’re working with. OLS is a great starting point because:
This basically means that as long as our data is not nonstationary (autocorrelation) and errors do not change variance over time (heteroskedasticity vs homoscedasticity), we are good to go; the data normality and linearity assumptions can actually be disregarded here.
The major advantage of OLS is its simplicity, due to the fact it just estimates the conditional mean of the dependent variable by minimising the sum of squared residuals:
where (another advantage) the closed-form solution is:
where, X is the n×p design matrix (with n observations and p predictors), y is the n×1 vector of responses, and X′X is the p×p Gram matrix (cross-product of predictors).
The simplicity of OLS, combined with its ability to predict signals directly in terms of trend (e.g., positive or negative expected returns), has made it a popular choice across the board—even among large quant hedge funds. Another key advantage is its interpretability: the coefficients in an OLS model represent the marginal effects on the mean return (as shown in the simple model below). This transparency ensures we avoid the pitfalls of falling into a 'black-box' scenario, where the inner workings of the model become opaque.
However, there are a few basic caveats to keep in mind with OLS:
Sensitivity to Outliers: OLS isn’t particularly robust to outliers, which can skew results.
Multicollinearity: LS struggles when working with many factors, especially if they’re correlated. This increases model complexity and raises the risk of overfitting. Fortunately, there are ways to address this issue, which we’ll explore later
Additionally, in my experience, OLS tends to lose predictive power when applied to lower-frequency data (you may have different opinions!).
That said, these limitations don’t render OLS obsolete. Instead, they encourage us to explore other algorithms that can complement or improve upon its performance, allowing us to make more informed comparisons.
Quantile regression has even fewer assumptions (e.g., no need for homoskedasticity) and - as you may expect - is way more robust to outliers. This stems from the fact that QR estimates conditional quantiles (e.g., median, 5th percentile) by minimising a weighted sum of absolute residuals:
where τ ∈ (0,1) is the target quantile. QR is generally very useful for risk modelling, as using it we can examine the behaviour of asset returns at different quantiles. For instance, assuming τ = 0.05, we can run the estimator below:
and check how our factor x affects the 5th percentile return, e.g., a crash risk.
The downsides of quantile regression mostly concentrate on its computational complexity, since the loss function has no closed-form solution, hence needs to be optimised using linear programming. In addition, if ideal conditions are met in terms of the data we work with, OLS will, on average, beat QR, as quantile regression basically sacrifices efficiency for robustness, as can be deducted from the formulas above.
Truth be told, considering advantages and disadvantages of both methods, it is still best just to compare both algorithms given the data we work with and then decide.
Ridge regression is another popular estimator due to its capability of tackling the multiple factor issues that OLS has. Assuming we want to use many factors that, in finance, tend to be correlated, OLS can easily lead to overfitted predictions. I don’t want to spend too much on this but given the closed-form solution we know:
when many factors are correlated X′X becomes nearly singular (i.e., its determinant is close to zero). This makes the inversion (X′X)−1 unstable. Why? Since OLS variance is calculated as:
when X′X is nearly singular, the diagonal elements of (X′X)−1 (which correspond to the variances of the coefficients) become very large. This basically leads to: unstable coefficient estimates (i.e., small changes in the data can cause large changes in β^OLS), and overfitting (the estimator fits noise in the training data, leading to poor generalisation). For more granular mathematical evidence ask google or deepseek.
This is where Dr Ridge kicks in. It works similarly to OLS (thus has its advantages) but additionally uses a shrinkage penalty to solve the aforementioned high dimensionality and multicollinearity problem:
where the closed-form solution is:
where, again, λ ≥ 0 is the regularisation strength, the expression after “+” is the shrinkage penalty, and I is the identity matrix. Thanks to this part: λI, it is ensured that X′X+λI is always invertible, even if X′X is singular. In addition, the variance of the Ridge estimator is reduced:
because λI shrinks the eigenvalues of X′X.
To simplify, the shrinkage penalty:
reduces coefficient variance which makes the estimator less sensitive to noise in the data which improves the generalisation to new data,
prevents numerical instability (X′X+λI) and allows the estimator to produce reliable coefficient estimates.
Naturally, by making λ = 0 we just go back to OLS; then again if we make it larger coefficients shrink more which reduces variance but increases bias (i.e., our estimator has trouble “learning”). This is also - I believe - a disadvantage of Ridge vs OLS; by introducing the shrinkage penalty itself we slightly increase the complexity of the model, as well as we must find the λ that best trades off between variance and bias. A good rule of thumb is to start with 0.1 if our factor space is not that large while possibly do 0.5 if we work with many factors (I think sklearn has 1.0 as default but I am not sure if it’s optimal).
With that, I think we’ve covered enough ground on the best linear algorithms available. Now, it’s time to shift our focus to nonlinear estimators. After exploring these, we’ll finally circle back to answer the central question posed in the title of this article.
Nonlinear estimators part
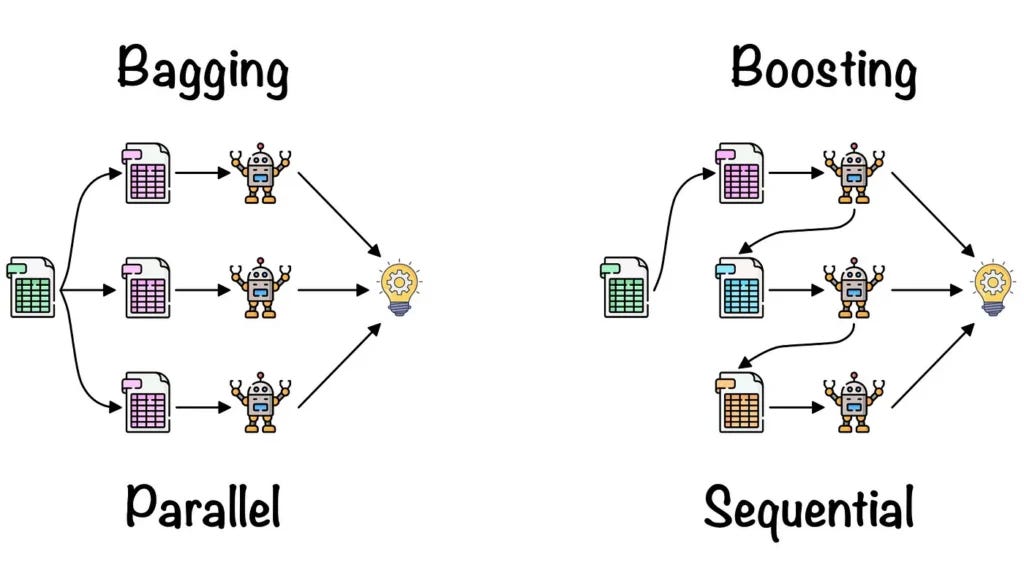
I don’t really want to focus on various models like Random Forest, XGBoost, LightGBM, Catboost, WTFBoost, etc., not to mention neural nets. I would rather just dive into the two most popular nonlinear methods: bagging and boosting, and take it from there.
To begin with, the reason why bagging and boosting methods are called nonlinear is because they use more complex than OLS, flexible models (e.g., decision trees) that can capture intricate, nonlinear patterns and interactions in the data. Unlike linear models, which rely on a fixed parametric form (see OLS formula above) bagging and boosting construct their predictions by combining multiple simple models in ways that adapt to the underlying structure of the data, allowing them to model highly nonlinear relationships effectively. This is a crucial fact that will be of help later but let’s forget about it for a moment.
Coming back to reducing variance that is important to tackle overfitting, bagging reduces it by averaging predictions from multiple models (almost always decision trees) trained on bootstrap samples. Mathematically, this goes as following: for B iterations, draw a random sample with replacement from the training data, and then aggregate predictions by averaging them (regression) or taking majority votes (classification):
where f^b(x) is the prediction from the b-th bootstrap sample. To make it more interesting, each sample is often drawn with replacement, meaning some observations may appear multiple times, while others may be left out. These different bootstrap samples are used to train separate estimators, and since the samples are slightly different, the trained estimators will also differ slightly. How this helps? Well, a variance of a single model x is expressed as:
which measures how much the predictions f^(x) fluctuate across different training datasets. Subsequently, when we average B models, the variance of the bagged predictor f^bag(x) is:
AND if the estimators are independent (or at least uncorrelated, which random sample replacing helps with), the variance reduces to:
This shows that the variance of the bagged predictor is reduced by a factor of B compared to a single model. In practice, the decision tree estimators are not independent due to sample overlapping but they are at least less correlated which still achieves a significant variance reduction.
So, if we have enough B estimators (the famous n_estimators parameter) we can reduce overfitting, even if we work with many factors, due to, again the random sample replacement. Some more advanced tree-based estimators, like Random Forest, use random feature selection which takes into consideration only a random subset of features. In other words, we can toss in a bunch of these, and RF will figure it out, no matter if correlated or not → still, in my opinion and experience, it is not the best idea to just “throw” a bunch of features there. Below is an example RF model which predicts stock volatility:
The caveat of bagging is obviously its complexity vs linear models and it being computationally expensive for large B. Even though this can be parallelised, it is still not as fast as calculating loss function of OLS. Then again, they are great for a data with a lot of noise and their interpretability is better than the next popular nonlinear algorithm: boosting.
Boosting mainly differs from bagging by improving predictions via focusing on errors from previous models, instead of horizontally aggregating them. Mathematically, let’s build an additive model by combining weak learners (e.g., shallow trees) iteratively:
where hm(x) is the m-th weak learner, and αm is its weight. Now, (gradient) boosting minimises a differentiable loss (e.g., squared error, quantile loss):
where y is the true target value and f^(x) is the predicted value; then at each iteration m, fits hm(x) to the residuals (negative gradient):
where r_i,m are residuals at each iteration m; and finally updates the current shallow estimator predictions by adding the predictions of the weak learner as:
where ν is the learning rate (shrinkage parameter). Here is a graph how it looks like in general and how it differs from bagging:
In other words, one tree is built, the algorithm checks how much it sucks, so another tree is built to correct the mistakes of the previous tree.
Below is an example (gradient) boosting model set up to predict credit risk, shown also for the sake of indicating the difference between boosting and bagging (again):
The major advantage of boosting over bagging, is that it has a higher target accuracy, as it iteratively corrects errors; then again, this is a straight path to overfitting, thus boosting requires more effort in terms of regularisation. However, boosting-based estimators are significantly faster to train due to their sequential nature. I believe the choice between both algorithms just depends on the data → if there is a lot of noise, I would go for bagging. Sometimes I see the contrary, that bagging is not recommended for noise but in my humble opinion it’s a total b****t, since that’s the point of bagging.
Alright, now that we’ve walked through this detailed explanation, it’s time to dive into the final section of the article and tackle the core question: When should we use which algorithm, and why?
When and why
This part of the article moves away from theory (at least partially) and sticks to practice. The major division between both methods lie between their ultimate purpose: do you want to trade the signals or do you want to just see the signal?
From what I have experienced and confirmed in X posts from many great folks, when you need a signal to trade directly, you should always start with a linear regression to obtain it. It does not mean you will get perfect expected returns BUT more often than not, you will get a correct trend and that’s gold. The path from this signal to actually trading it is a bit more complicated though: often quants put advanced algorithms on the top of that in order to deal with false flags, optimize weights, and so on. However, the signal itself is simple (as the math above shows)!
The only thing I would always consider is the choice of the linear method mentioned in the previous section. Even though, according to the Gauss-Markov theorem, OLS does not give a single F about data distribution (it’s all about residuals, remember?), if you deal with a lot of assets that have various distributions (sometimes much skewed or having tails fat as Nancy Pelosi’s portfolio), it may be better to begin with quantile regression. Still, obviously, it’s best to compare but my money is on QR here. Finally, if you work with many factors, then start with Dr Ridge. Go back to the math above if you want to ask why.
HOWEVER, in terms of calculating the signal to trade directly, it is not ALWAYS best to go for a linear algorithm. If you work with huge datasets (HFT) and have containers of GPUs (like sir XTX), I would honestly go for neural nets here. These guys, if constructed correctly and applied to abundant datasets, can often beat OLS & co; although, sometimes the magnitude of outperformance is not significant, hence why would you bother?
Finally, I’d consider tree-based methods as a last resort for trading signals. The reason is simple: more straightforward approaches often outperform them in this context. That said, there’s one area where I’d prioritize using trees—asset allocation (AA) and related learn-to-rank algorithms. This is because AA typically involves working with lower-frequency data, a topic I’ll touch on later as we dive into nonlinear methods.
Through my extensive work in quantitative research, I’ve observed a consistent pattern: on average, the lower the frequency of the data, the better nonlinear algorithms tend to perform compared to linear ones. However, this observation comes with a paradox: sample size. Lower-frequency data inherently means fewer data points, which typically favours linear models, as they often excel with smaller datasets. That said, this hurdle can be overcome by combining multiple assets into a panel dataset, allowing us to work with weekly or monthly frequencies while maintaining a sufficiently large sample size (boosting here may be of better help if we want to work with the likes of Russell 3000).
So, why do nonlinear algorithms often outperform at lower frequencies (IMHO)? I believe it’s tied to how the factors we use behave over different time horizons. In higher-frequency data, the movement from one point to another tends to be smoother and more linear. In contrast, lower-frequency data captures larger, more abrupt shifts—what I call 'kinks' in the series—as a lot can happen over weeks or months. These shifts often reflect cumulative effects, regime changes, or threshold behaviours that linear models struggle to capture.
In addition, the relationships between features often (NOT ALWAYS) move away from linear to nonlinear the lower the frequencies. This is because lower-frequency data smooths out short-term noise, revealing the underlying, longer-term dynamics that are often governed by complex, nonlinear interactions. For example, factors like valuations, interest rates or inflation may have linear effects in the short term but exhibit nonlinear behaviours over longer horizons due to feedback loops, saturation points, or regime shifts.
All of this sounds great, but as you read it, you’ll notice a shift in focus: we’re moving away from trading and into research. This gradient isn’t just something I’ve observed in my own work—it’s something I’ve seen in 90% of pro fintwit discussions too: when it comes to trading, it’s better to stick to linear methods, but when the goal shifts to generating and interpreting signals, nonlinear approaches tend to take the lead. This is especially true when we move from regression to classification, where the focus is on estimating the probability of a specific event occurring.
The goal here isn’t necessarily to trade directly off these signals but to gain insights and prepare for potential next steps. This approach naturally aligns with lower-frequency data, as high-frequency trading often leaves little room for manual intervention—it’s better left to algorithms. One of the most effective ways to boost the accuracy of these 'slower' signal-generation methods is by blending machine-driven insights with human expertise, creating a quantamental approach. I can’t stress enough how often I’ve seen this combination winning the game over the long term, whether in equities, bonds, or FX.
As to which algorithm works better: bagging or boosting, I usually find boosting to outperform. I guess, it’s simply because of the math shown in the previous section → boosting tends to be more accurate but can overfit more, yet we can regularise it easily to reduce variance (see my X post here).
The only exception from this rule is the aforementioned asset allocation and using nonlinear methods to generate direct trading signal (with some optimisation overlay that I mentioned above). I’ve seen too much greatness from learn-to-rank and talked to some big players confirming it. Still, it’s always good to run linear methods as well and compare.
Short summary
That’s it, I am out of carrots. Let’s summarise my thoughts:
Linear for trading the signal directly.
Nonlinear for research and generating signals to interpret them.
Check out the math from the first section to help you understand why.
Thank you for your attention.


Great write up, very thorough
I would love to present the AI Factor from Portfolio123.com to you and do a video interview with you about what you think about it. My experience so far --> linear is fine if you want to produce low vola systems (Procter & Gamble has linear kind of data). Non-linear MLs (NVDA was a right tail event in terms of earnings acceleration) if you want to build total return systems (especially on small caps). One thing is important with nonlinear ML Algos --> you need tons of data (>20 Years)...